| ENG RUS | Timus Online Judge |
1137. Bus RoutesTime limit: 1.0 second Memory limit: 64 MB Several circular bus routes were in the city of Fishburg. None of the routes shared the same section of road, though common stops and intersections were possible. Fishburg old residents stated that it was possible to move from any stop to any other stop (probably making several transfers). The new mayor of the city decided to reform the city transportation system. He offered that there would be only one circular route going through all the sections where buses moved in the past. The direction of movement along the sections must be the same and no additional sections should be used.
Write a program, which creates one of the possible new routes or finds out that it is impossible.
InputThe first line contains the number of old routes n (1 ≤ n ≤ 100). Each of the following n lines contains the description of one route: the number of stops m (2 ≤ m ≤ 200) and the list of that stops. Bus stops are identified by integers from 1 to 1000. A route is represented as a sequence of m + 1 bus stop identifiers: l1, l2, …, lm, lm+1 = l1 that are sequentially visited by a bus moving along this route. A route may be self-intersected. A route always ends at the same stop where it starts.
OutputThe output contains the number of stops in the new route k and the new route itself in the same format as in the input. The last (k+1)-th stop must be the same as the first. If it is impossible to make a new route according to the problem statement then write 0 (zero) to the output. Sample
NotesHere is a picture for the example: 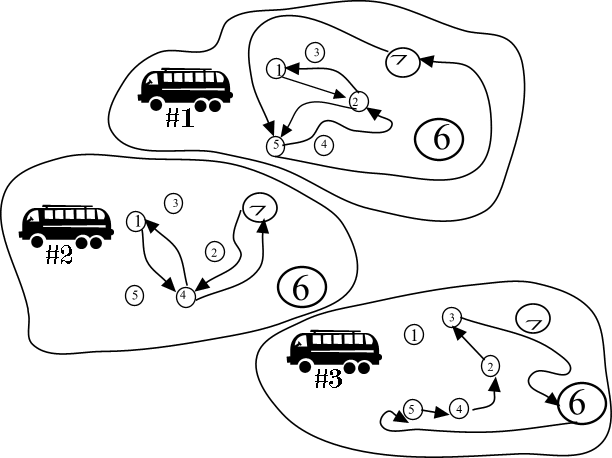 Problem Source: Quarterfinal, Central region of Russia, Rybinsk, October 17-18 2001 Tags: graph theory |
