| ENG RUS | Timus Online Judge |
1231. Turing: One, Two, Three, …Time limit: 1.0 second Memory limit: 64 MB 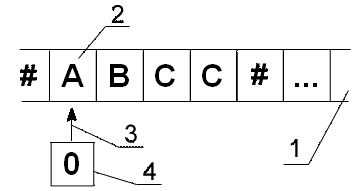 A Turing machine used for computability research is well known to computer scientists. We will give a brief description of this abstraction. Turing machine is an automatic device that works on a tape (1) of potentially unlimited length. The tape is divided into cells each containing a character. One of the cells is called a viewed, or current, one (2). At any point of time the Turing machine has a condition that is stored in the control unit (4). Besides, the read/write head (3) of the control unit is pointing to the current cell. The control unit can execute one action per time interval (step). The action includes a state change, a possible change of the character in the current cell, and a possible movement to the adjacent cell. These actions are defined in a special table, called a control table. We will denote the movements along the tape with the following symbols: "<" — to the left, ">" — to the right, "=" — no movement. The control table is actually a program for the Turing machine. The work of the Turing machine is considered to be done if no line in the control table contains the combination of the current character and condition.
Control table example:
Notice. This example only illustrates the definition of the table.
The input data for the Turing Machine are placed beforehand in the cells of the tape. The result is written to the same tape. Assume that the initial condition for the Turing machine is equal to 1 and the input data on the tape are bounded on both ends with '#' characters. (All tape cells except those that filled with minuses are filled with '#' character.) The control block is placed at the leftmost '-' character of the input data. The input tape contains '-' (minus) character repeated n times Imagine that the minuses are placed in circle. Starting with the first one each k-th uncrossed minus is crossed, i.e. it turns into a '+' (plus). The execution stops when there is only one uncrossed minus is left. Your task is to describe the control table for the Turing machine that will cross all minuses except one (it's position defined according to the above algorithm, but you may use any method) for the given k. For example, for n = 10 and k = 3 the fourth minus will remain uncrossed. You may place the following characters on the tape: '+', '#', 'A'..'Z'. The cells initially filled with minuses may only contain '-' and '+' characters. After the execution the read/write head must point to the uncrossed minus. The number of the steps s must not exceed 1 000 000. The number of the line in the control table p must not exceed 10000. Tape size limited with 10001 cells (5000 both side from the initial read/write head position).
InputThe input contains an integer number k (1 ≤ k ≤ 200). OutputThe output describes the control table for the Turing machine for the given k. The first line of the output contains the number of rows p in the table Sample
NotesNote, that this example is correct only for n = 2. It just shows output format. Problem Source: 2002-2003 ACM Central Region of Russia Quarterfinal Programming Contest, Rybinsk, October 2002 Tags: none |
