| ENG RUS | Timus Online Judge |
1318. LogarithmTime limit: 1.0 second Memory limit: 64 MB Given a set A of N unordered 128-bit numbers. You are to compute a value of the function 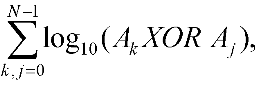 where Ak is the kth element of A, log10X — the integer part of the decimal logarithm of X. We’ll assume that log100 = 0. InputThe first input line contains a number N ≤ 5000. In the following N lines there are 128-bit numbers Ak presented by sets of numbers (a1k, a2k, a3k, a4k), each of them lies in range from 0 to 232-1. The number Ak can be obtained from this set according to the formula Ak = 296a1k + 264a2k + 232a3k + a4k. OutputYou are to output the value of the function for the given set. Sample
Problem Author: Idea: Nikita Shamgunov, prepared by Nikita Shamgunov, Anton Botov Problem Source: VIII Collegiate Students Urals Programming Contest. Yekaterinburg, March 11-16, 2004 Tags: none |
