| ENG RUS | Timus Online Judge |
1497. Cutting a SquareTime limit: 1.0 second Memory limit: 64 MB After Vasya has finished his homework, he devotes himself to the following puzzle. He takes a white sheet of squared paper of size N × N cells,
selects a non-empty connected subset of cells, and paints this subset black. When he has cut out the black piece, exactly one white piece is left. Then Vasya reunites the pieces into the original square and puts it onto an infinite table. Now his task is to
disjoin the pieces by moving one of them along the table surface far from another in such a way that both pieces always stay in total contact with the table. For example, in the figure there are squares 5 × 5. In the first case the pieces
can be separated and in the second case this is impossible. 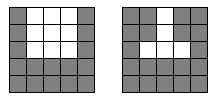 Once Petr came to visit Vasya. He saw Vasya's occupation and wanted to help his best friend by writing a program that determines if the black and white pieces can be separated. InputThe first line contains the integer N
(3 ≤ N ≤ 1000). In the next N lines containing N symbols each, the colors of the square's cells are given. Symbols 0 denote white and symbols 1 denote black. It is guaranteed that both pieces are connected with respect to cells' sides (for example, two cells with a common vertex but without common sides are not considered to be a connected piece). OutputOutput “Yes” if the pieces can be separated, and “No” otherwise.
Samples
Problem Author: Alexander Toropov Problem Source: XIII-th USU Junior Contest, October 2006 Tags: none |
