| ENG RUS | Timus Online Judge |
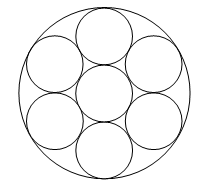
1660. The Island of Bad LuckTime limit: 0.5 second Memory limit: 64 MB The natives of an island in the Pacific between 35 and 36 degrees
of southern latitude have the following custom. The chief of the tribe draws
a large circle with radius R on the sand, and inside it he draws another one
with radius r. The distance between centers of the circles is equal to d.
The chief's wife (let's call her victim) inscribes a circle in such a way,
that it touches the bigger one from within and the smaller one from the
outside. Then all of the tribe members come to the circles in turns and each
of them tries to inscribe a circle in such a way, that it would touch both
of the chief's circles and the circle, which was drawn the latest. The circle
must not intersect any other circles, except touching the one, drawn by victim.
If a native can inscribe his circle in several ways, he asks the victim for
advice (remember, that as a chief's wife she has a great authority among
natives). When no more circles can be inscribed, the distance between the first
and the last inscribed circles is measured. This distance determines, whether
the victim will be eaten. So, she really needs to know the least possible
distance between these circles.
 Input3 integers: R, r and d.
0 < r < R − d. d ≥ 0.
Numbers don't exceed 100.
OutputOutput the required distance with not less than 5 digits after the decimal point.
Sample
Problem Author: Alexander Kokovin (prepared by Alexander Ipatov) Problem Source: Ural SU Contest. Petrozavodsk Winter Session, January 2008 Tags: geometry hardest problem |
