| ENG RUS | Timus Online Judge |
1689. Fisherman and BarbellTime limit: 1.0 second Memory limit: 64 MB 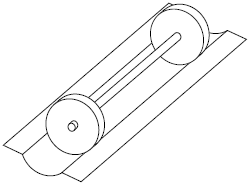 Fisherman Ivan likes to practice weightlifting when he is free from fishing.
He lifts the barbell, turns, twists, and spins it, and does everything he wants
with it. During these tricks the special semicircular groove in which
the barbell is usually kept stays free and worms crawl into it. Ivan doesn't want to
squash the worms because he will need them as a bait for fishing. That is why
he chooses the place to put the barbell in such way that it hurts as few worms as possible.
Can you find such a place?
There is a p cm wide plate on each side of the barbell. The distance
between the left edge of the left plate and the right edge of the right plate
is b cm. The length of the groove is g cm.
All worms have the same length w cm and lie along the groove on its
bottom without overlapping. If even a small part of a worm gets under a plate
of the barbell, it is considered squashed and is unfit for fishing.
InputIn the first line you are given the length of the groove g
and the length of a worm w (1 ≤ w ≤ g ≤ 100000).
In the second line there are the characteristics of the barbell
b and p (1 ≤ p ≤ b/2 ≤ g/2).
The third line contains the number of worms n
(1 ≤ n ≤ 100000).
In the fourth line you are given the coordinates of the worms
xi separated with a space; they are in the range from 0
to g − w. The coordinate of a worm is the distance from its
left end to the left end of the groove in centimeters.
All numbers in the input data are integers.
OutputOutput the integer distance from the left edge of the left plate of the barbell
to the left end of the groove in centimeters. The barbell should hurt the
minimal number of worms. In the case of equal number of the hurt worms, the
distance to the left end of the groove should be minimal.
Samples
Problem Author: Stanislav Vasilyev Problem Source: USU Open Personal Contest 2009 (February 28, 2009) Tags: none |
