| ENG RUS | Timus Online Judge |
1765. Error 404Time limit: 3.0 second Memory limit: 64 MB Experienced participants of the Ural Championship come to Yekaterinburg in
advance to get accustomed to the severe weather conditions, walk around the
city, and, of course, visit the “Limpopo” Water Park. Not many people know
that there is Plant No. 404 near the water park, and this plant is called
“Error 404” by the locals. The plant is not easy to find indeed, and it is
still more difficult to learn what is happening there. Fortunately, one can
watch the plant from a nearby pedestrian bridge. Because of the seeming
stillness and desolation of the plant, one may think that it is out of
operation, but this is not so. The main work area of the plant is the repair of
aviation engines.
Some time ago the plant received an order to repair a broken gas turbine
engine. It turned out that some blades were torn off, which resulted in an
excess load on the engine shaft. Experts at the plant have decided that the
engine could be repaired quickly by removing some of the intact blades so that
the center of masses of the remaining blades would be on the rotation axis once
again. To keep the engine power as large as possible, a minimum number of
blades should be removed. At least one blade must be left, otherwise the engine
would not work at all. The experts assert that when all the blades were intact
their endpoints formed a regular 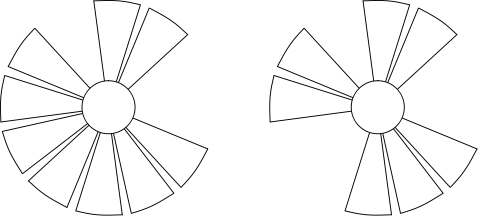 InputThe first line contains the initial number of blades in the turbine n
and the number of torn blades k ( OutputIn the first line output the minimum number of blades that should
be removed. In the second line output the numbers of these blades in any order
separated with a space. If several answers are possible, output any of them. If
it is impossible to repair the engine by removing some of the blades,
output “−1”.
Samples
Problem Author: Igor Chevdar (idea by Dmitry Poletayev) Problem Source: The 14th Urals Collegiate Programing Championship, April 10, 2010 Tags: none |
