| ENG RUS | Timus Online Judge |
1799. Sasha and swag stringsTime limit: 2.0 second Memory limit: 256 MB Sasha enjoys strings and problems on string theory. Especially he loves suffix structures. As Sasha loves TopForces community he is going to write an entry named “On suffix trees, part 37”. Surely, he wants everybody to understand what the article says, so he decided to decorate it with some nice examples. After a recent contest on TopForces, Sasha has achieved the rank “International swagger”, and now he wants to match it. To achieve this, Sasha wants to choose the swaggest strings among some given set. Of course, Sasha’s concept of string swagness is based on suffix structures. To be precise, on suffix trees. To calculate the swagness of a string, Sasha performs the following actions:
The swagness of the string is defined as the sum of the calculated values among all edges. Unfortunately, Sasha is not so good with the suffix trees as he wants you to think, and can’t handle the problem on his own. Help him! InputThe first line contains an integer n (1 ≤ n ≤ 105). Each of the next n lines contains a string. The i-th line contains a non-empty string si. Each string consists entirely of lowercase Latin letters. The total length of all strings si does not exceed 105. OutputPrint n integers, one per line. The i-th number must be the swagness of the string si. Samples
NotesCompressed suffix tree for string abaaa: 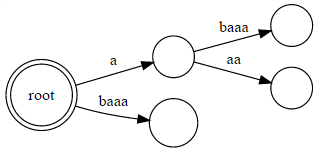 Edges are a, aa, baaa and baaa. They have 1, 2, 7 and 7 distinct non-empty substrings, respectively. So, the answer is 1 + 2 + 7 + 7 = 17. Problem Author: Oleksandr Kulkov Problem Source: Petrozavodsk Summer 2015. Moscow IPT Contest Tags: string algorithms |
