| ENG RUS | Timus Online Judge |
1849. Rabbit Hunt 2Time limit: 4.0 second Memory limit: 64 MB A good hunter kills two rabbits with one shot. But you need to kill the maximal possible number of
rabbits with one shot to become the best hunter in the world. The program Rabbit Hunt 2 might be
quite helpful. This program treats all rabbits as points on a plane. It reads coordinates of n rabbits
from the input, generates q different shooting propositions and chooses the one which leads to killing the maximal
number of rabbits. A shooting proposition is defined by coordinates of the hunter and the direction of shooting.
The shot kills all the rabbits lying on the corresponding ray including the rabbit situated at the same point as the hunter. A proposition generator uses numbers ax, bx, ay, by, avx, bvx, avy, bvy.
Coordinates of the hunter in the first proposition is (x1, y1), and a direction of shooting is (vx1, vy1).
Coordinates and direction in the i-th proposition (i > 1) are calculated using these formulas: 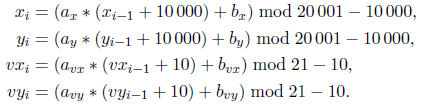 Unfortunately, the program Rabbit Hunt 2 doesn't exist yet. Your goal is to create it. InputThe first line contains a number of rabbis n (1 ≤ n ≤ 10 000). The next n lines contain
the coordinates of rabbits. Coordinates are integers not exceeding 10 000 in their absolute value.
No two rabbits are situated at the same point. The next line contains a number of shooting
propositions q (1 ≤ q ≤ 106). The next line contains integers x1, y1, vx1, vy1
OutputOutput the number of proposition resulting in the maximal quantity of killed rabbits and this quantity.
If there are several such propositions, output the one with the maximal number. Sample
Problem Author: Alex Samsonov Problem Source: Ural SU Contest. Petrozavodsk Summer Session, August 2010 Tags: none |
