| ENG RUS | Timus Online Judge |
1870. Zinium 2Time limit: 1.0 second Memory limit: 64 MB As you remember, Zinium is a chessboard of size n × n cells. The
cell in its bottom left corner has coordinates (1, 1), and the cell in its
top right corner has coordinates (n, n). According to a legend, if n
queens are placed on the board so that none of them attacks another, the
released energy of Zinium will change the world beyond recognition. Rivers
will turn back, the sky will fall onto the earth, people will learn to
call things by their proper names… 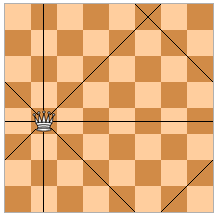 Everybody had believed the legend about Zinium until Igor got hold of the
artifact. He managed to place n queens as required but nothing happened
(at least he didn't notice anything unusual). Then Igor conjectured that
the chessboard in the legend was not usual but toric. A toric n × n
chessboard is obtained from the usual chessboard of the same size by
gluing together its upper and lower ranks as well as its leftmost and
rightmost files. The figure shows the cells of a toric 8 × 8
chessboard attacked by a queen. Igor wants to check his conjecture by
placing n queens on the toric board so that none of them attacks
another. Help him to do this. InputThe only line contains the integer n (4 ≤ n ≤ 105). OutputIf the queens can be arranged as required, output “Yes” in the first
line and n integers in the second line.
The ith number must be the y coordinate of the queen whose x
coordinate is i. If there are several possible arrangements,
output any of them. If the queens can't be arranged as required, output
“No” in the only line. Samples
Problem Author: Igor Chevdar (prepared by Eugene Kurpilyanskiy) Problem Source: Open Ural FU Championship 2011 Tags: none |
