| ENG RUS | Timus Online Judge |
2053. BiologyTime limit: 1.0 second Memory limit: 64 MB Android Vasya prepares a research work in Biology.
In this work he studies the class of arachnoid. Vasya is not interested in spiders themselves,
his work is mostly concentrated on the webs made by different species of spiders. Vasya has already found out how the web is made.
It is a set of points — the web knots, connected with each other by the so-called fibres.
One may imagine the web knots as coplanar points.
The web fibres are line segments, connecting the knots.
An important property of these segments is that they cross only in the knots. 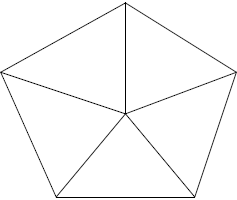 Vasya wants to determine which spiders make webs with the highest quality.
For this purpose he defined the stickiness of the web as amount of different traps in it.
A trap is a polygon with no self-crossings and self-tagencies, where knots of the web are vertexes and fibres are edges. Vasya has analysed several webs with 16 knots.
As a result, he has discovered that stickiness of those webs is between 5 000 and 300 000.
And now he is interested in finding out how a web with 16 knots and stickiness more than 300 000 can look like. InputThere is no input data in this task. OutputIn the first 16 lines output coordinates of the web knots as pairs of integers xi, yi (−1000 ≤ xi, yi ≤ 1000).
In the next 16 lines output an adjacency matrix of the web — the table of a size 16 × 16, composed of the symbols “0” and “1”.
The matrix should be symmetrical and its main diagonal should be filled with zeros. Any two knots of the web should lie in different points. Knots mustn’t lie on the inner points of the fibres.
Any two fibres may cross only in their common knot. The web should have stickiness more than 300 000. It is guaranteed that such webs exist. Sample
NotesThe answer in the example is not correct and just illustrates the answer format.
Note, that you should output the web with 16, not 6, knots.
The picture above corresponds to this example.
The stickiness of the web in the example is only 21. Problem Author: Alexander Ipatov Problem Source: Ural Sport Programming Championship 2015 Tags: unusual problem |
