| ENG RUS | Timus Online Judge |
2076. VasianaTime limit: 2.0 second Memory limit: 256 MB Vasya drew a set of points (x0, y0) on the plane such that, for each (x0, y0), there exists at least one real t with a · t2 + b · t + c = x0 and d · t2 + e · t + f = y0. This curve was very interesting: it had the axis of symmetry and maybe not only one!
Vasya realized that he obtained a new scientific result and decided to name this curve Vasyana. During the analysis of the mathematical characteristics of Vasyana, he drew a point P = (Px, Py) on the plane and then drew the perpendicular from P to the one of the Vasyana symmetry axis. Let Q be the base of this perpendicular. Is it true that a circle with center at the point Q and with radius R has common points with Vasyana? 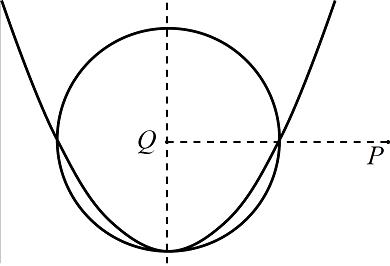 InputThe input contains several tests. In the first line you have an integer T, which is the number of tests (1 ≤ T ≤ 7000).
Then you have T blocks. Each of them has three lines with tests in the following format: a b c d e f Px Py R There are only integers in the input and their absolute values are not greater than 1020. R ≥ 1. OutputIf it is guaranteed that the circle and the Vasyana have a common point, output “YES”.
If it is guaranteed that the circle and the Vasyana have no common points, output “NO”.
If it depends on which axis of symmetry has been chosen, output “MAYBE”.
It is guaranteed that Vasyana has at least one axis of symmetry. Sample
NotesThe circle with the center in the point P and with the radius R is defined as the set of points such that the distance between P and each of these points is not greater than R. The Vasyana in the example is the parabola y = x2. It has only one axis of symmetry x = 0. You can see on the picture that a part of this parabola lies inside of the circle with the center Q = (0, 1) and the radius 1. Problem Author: Mikhail Rubinchik Tags: geometry hardest problem |
