| ENG RUS | Timus Online Judge |
Ural Regional School Programming Contest 2011
Contest is over
F. Rubinchik's CubeTime limit: 0.5 second Memory limit: 64 MB  Striving to develop their intellectual skills, the players of the Psych Up
team decided to learn how to solving a Rubik's cube. After a week, they
gave up the attempt in despair. Instead, they decided to solve a simpler
2 × 2 × 2 Rubik's cube but also failed. Then the team leader
Misha invented a cube that was even simpler. The new cube consists of four layers of size 4 × 4. Each layer is
made of glass and is absolutely transparent. The upper face of each layer
is divided into 16 equal squares. Four of them are painted red, yellow,
blue, or green. There is a hole at the center of each layer. A solid rod
is put through the holes so that the layers can be turned independently of
each other. The layers look as follows. 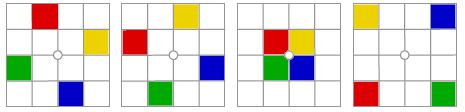 The cube is solved if it is in one of the following states (top view). 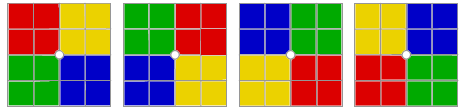 It was hard to solve the cube, but the Psych Up team did it. Your task
will be even harder! You must solve the cube from a given state in a
minimum number of turns. One turn is a turn of one layer by 90 degrees in
any direction. InputYou are given four lines, each containing four integers, which describe
the current state of the cube (top view). The numbers are in the range
from 1 to 4; they correspond to the colors of the cube's squares.
Different numbers denote different colors. OutputOutput the minimum number of turns needed for solving the cube. Sample
Problem Author: Denis Mukhametianov Problem Source: Ural Regional School Programming Contest 2011 |
