| ENG RUS | Timus Online Judge |
NEERC 2011, Eastern subregional contest
Contest is over
C. Frequent Flyer CardTime limit: 1.0 second Memory limit: 64 MB The Oceanic Airlines company has presented a new product for its regular
customers—a frequent flyer card. If a passenger shows this card at
check-in, one tenth of the flown miles will be deposited onto the card. Later
the passenger can redeem the accumulated miles for a free Oceanic Airlines
flight, thus saving a considerable amount of money. For example, having bought
tickets for flights from Yekaterinburg to Frankfurt, from Frankfurt to New
York, and from New York to Orlando, the passenger can later get a ticket for a
flight from Yekaterinburg to Warsaw for free. Each frequent flyer card has a unique number consisting of n + 1 decimal digits.
The first n digits can be arbitrary (let us denote them by x1, …,
xn). The last digit is a check digit; it is calculated by the formula 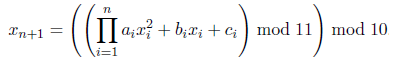 where (p mod q) is equal to integer r such that (0 ≤ r < q) and q divides (p − r). The card numbers are produced by the following algorithm: each of the first n digits
is chosen uniformly at random from 0 to 9, independently from each other, and then
the last digit is
calculated according to the above formula. The company management wants the
last digits of the first 10 sold cards to be pairwise different. How many card
numbers should be generated on average to obtain among them 10 numbers with
pairwise different last digits? InputThe first line contains the integer n (2 ≤ n ≤ 25).
The second line contains the integers a1, …, an, the third
line contains the integers b1, …, bn, and the fourth line contains
the integers c1, …, cn (0 ≤ ai, bi, ci ≤ 9). OutputOutput a real number, which is the expected number of generations of the first
n digits of the card needed for obtaining 10 cards with different last digits.
The absolute or relative error of the answer should not exceed 10−6. If
there are no 10 card numbers with pairwise different last digits,
output “-1”. Samples
Problem Author: Eugene Kurpilyanskiy Problem Source: NEERC 2011, Eastern subregional contest |
