| ENG RUS | Timus Online Judge |
Open Ural FU Personal Contest 2013
Contest is over
C. KiteTime limit: 1.0 second Memory limit: 64 MB Vova bought a kite construction kit in a market in Guangzhou. The next day
the weather was good and he decided to make the kite and fly it.
Manufacturing instructions, of course, were only in Chinese, so Vova
decided that he can do without it. After a little tinkering, he
constructed a kite in the form of a flat quadrangle and only needed to
stick a tail to it. And then Vova had to think about that: to what point of the quadrangle's
border should he stick the kite tail? Intuition told him that in order to
make the kite fly steadily, its tail should lie on some axis of symmetry
of the quadrangle. On the left you can see two figures of stable kites,
and on the right you can see two figures of unstable kites. 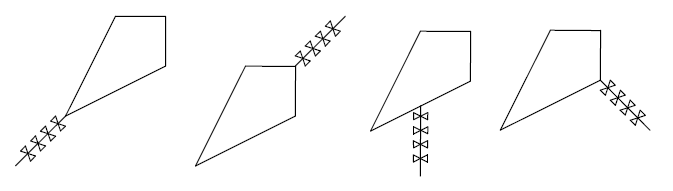 How many points on the quadrangle border are there such that if we stick a
tail to them, we get a stable kite? InputThe four lines contain the coordinates of the quadrangle's vertices in a
circular order. All coordinates are integers, their absolute values don't
exceed 1 000. No three consecutive quadrangle vertices lie on the same
line. The opposite sides of the quadrangle do not intersect. OutputPrint the number of points on the quadrangle border where you can attach
the kite. Samples
NotesThe axis of symmetry of a flat figure is a straight line lying in the figure plane and dividing the figure to the two halves that are each other's mirror image.
Problem Author: Alexander Ipatov Problem Source: Open Ural FU Personal Contest 2013 |
