| ENG RUS | Timus Online Judge |
USU Junior Contest October'2003
Contest is over
B. PoolTime limit: 1.0 second Memory limit: 64 MB 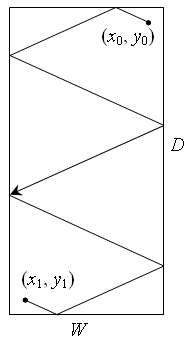 During the lunch-break the programmer Vasechkin likes to hack around his rectangular room. His way starts at his workplace and ends at the point where the thought to continue the work comes to his mind. We know that when Vasechkin runs against a wall he bounds according to the law “the angle of incidence equals to the angle of reflection”. Besides being a very straight person Vasechkin moves from wall to wall in the direct line segment. The baleful front office decided to find out how much time Vasechkin wastes during his promenades. It’s very easy to find out the time by dividing the length of the way that Vasechkin has passed over his average speed (that was measured by the front office beforehand). So it’s necessary to find out the way length! And since Vasechkin’s bumps are well-heard it’s sufficient to know the order of Vasechin’s collisions with walls. May be there is a more simple way to calculate the time wasted by the programmer but he front office believes that its solution of the problem is the most correct. InputThe first line consists of two integers W and D — they are the width and the depth of Vasechkin’s room in meters (2 ≤ W, D ≤ 1000). The second line contains the initial Vasechkin’s position coordinates (0 < x0 < W; 0 < y0 < D), measuring from the front-left corner of the room. The third line — the final position coordinates (0 < x1 < W; 0 < y1 < D), measuring from the front-left corner of the room. All coordinates are integers. The fourth line contains the sequence of letters L, R, F, B, denoting the sequential Vasechkin collisions with walls — the left, right, front and back one respectively. An amount of collisions doesn’t exceed 1000. The programmer never collides a corner of his room and his initial and final positions don’t lie on walls. OutputOutput the length of Vasechkin’s way from the initial point to the final one rounded to four decimals after the point. Sample
Problem Author: Pavel Egorov Problem Source: Open collegiate programming contest for high school children of the Sverdlovsk region, October 11, 2003 |
