| ENG RUS | Timus Online Judge |
USU Junior Contest, October 2006
Contest is over
A. Points on a ParallelepipedTime limit: 1.0 second Memory limit: 64 MB Petya wants to make a paper parallelepiped with dimensions
A × B × C.
He has already produced a surface map of the parallelepiped
(see figure): 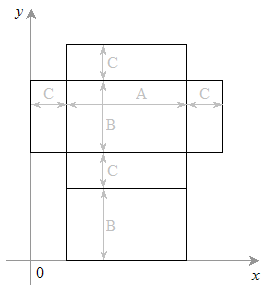 On this surface map Petya has marked two points with coordinates
(x1, y1) and
(x2, y2).
Can you find the distance between these points after the
parallelepiped is assembled? InputThe first line contains integers A, B, C
(1 ≤ A, B, C ≤ 1000).
In the second line there are the coordinates of the first point
(x1, y1),
and in the third line there are the coordinates of the second point
(x2, y2).
The numbers x1, x2,
y1, y2
are given with two fractional digits.
The points (x1, y1) and
(x2, y2) are different and
belong to the surface map. OutputOutput the distance between the marked points after the
parallelepiped is assembled, with accuracy to 10−6. Sample
Problem Author: Vladislav Isenbaev, Alexander Toropov Problem Source: XIII-th USU Junior Contest, October 2006 |
