| ENG RUS | Timus Online Judge |
NEERC, Eastern subregion, Yekaterinburg, October 2006
Contest is over
H. Difficult DecisionTime limit: 1.0 second Memory limit: 64 MB Often, when a decision about investing in a new business must be taken, a New Russian has to estimate quickly whether a certain project will be a success or not. Leading economists have recently discovered a new algorithm for forecasting the success of a project. First, one has to form an n × n matrix of risks. Let us denote this matrix by A. Then, in order to take into account the interdependencies of the parameters inside the matrix, the matrix 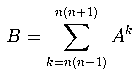 must be computed. If at least one of the elements of the matrix B is zero, then there is a considerable probability that the project will fail. Otherwise, if there are no zero elements in the matrix B, the new business will grow and flourish. Help New Russians to make use of this algorithm. Your task is to write a program that determines the probability of the success of a project given the matrix of its risks. InputThe first line of the input contains the dimension n of the matrix A (2 ≤ n ≤ 50). Each of the next n lines contains n numbers that forms the matrix A. Each element is a whole number in the range from 0 to 100. OutputOutput "No" if there is at least one zero element in the matrix B (so it is better not to invest in the new business). Otherwise, output "Yes". Samples
Problem Author: Evgeny Krokhalev Problem Source: Quarter-Final of XXXI ACM ICPC - Yekaterinburg - 2006 |
