| ENG RUS | Timus Online Judge |
Ural Championship 2010
Contest is over
J. Ski-Trails for RobotsTime limit: 1.0 second Memory limit: 64 MB One of the stages of the Robot Cross-Country World Cup was held at the Uktus
Ski Lodge in Yekaterinburg.
Professor Popov's laboratory sent its newest Robot NS6 to take part in the
race. The neural networks of this robot were well-trained in the classic style
skiing. The robot was not very lucky with the drawing: he was one of the last
racers to start and the trails had been already heaped up with the participants
who hadn't been able to make their way to the finish. This created a serious
problem, as the robot now had to keep switching between the ski trails in order
to skirt the obstacles. As a result, it lost the precious time because moving
to an adjacent trail each time took one second.
Given the places where the fallen robots lie, determine the optimal way to
skirt them all in the minimum time. 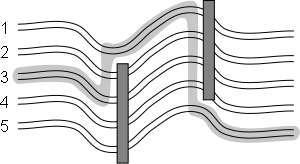 InputThe first line contains integers n, s, and k separated with a space (2 ≤ n ≤ 105; 1 ≤ s ≤ n;
0 ≤ k ≤ 105). There are n parallel
ski trails that lead from start to finish. They are numbered successively from
1 to n. Robot NS6 starts along the trail with number s. The integer k is the number of robots which fell down on the trails.
The following k lines describe the lying robots in the order from start to
finish. In each line there are integers l and r, which mean that a robot
blocked the trails with numbers from l to r inclusive (1 ≤ l ≤ r ≤ n). You can assume that all the fallen robots lie at a sufficient distance
from each other (and from the start) so that Robot NS6 can perform the
necessary maneuvers. If some robot blocks an outermost trail, it can be skirted
on one side only. No robot blocks all the trails simultaneously. OutputOutput the minimum time in seconds that Robot NS6 spent for switching from
trail to trail in order to skirt all the fallen contestants and successfully
complete the race.
Sample
Problem Author: Alex Samsonov Problem Source: The 14th Urals Collegiate Programing Championship, April 10, 2010 |
