| ENG RUS | Timus Online Judge |
2198. Deep UnderstandingTime limit: 1.0 second Memory limit: 256 MB Many years ago, Vadim heard the term “ordered rooted tree”. He understood what it was, but that was not enough for a “deep understanding”. Vadim sometimes refers to the height of a rooted tree as its “depth”, and just recently he decided to explore all possible ordered rooted trees of size N. After drawing them all on a single sheet of paper, he wrote the “depth” of each tree next to its corresponding drawing. Finally, Vadim achieved a “deep understanding” by summing all the written numbers. He called this value the “magnitude of deep understanding”. Your goal is to find this magnitude modulo 109+7. A tree is a connected graph without cycles. A rooted tree is a tree with a designated vertex (the root), which is usually drawn at the top of the graph. The height of a rooted tree is the maximum number of edges that can be traversed sequentially from the root without traversing any edge twice. An ordered rooted tree is a rooted tree in which the edges outgoing from each vertex are ordered. For example, the following two trees of height 2 are considered different: 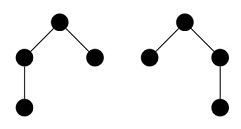 InputA single integer N is given, representing the size of the trees being considered, that is, the number of vertices in them (1 ≤ N ≤ 400). OutputOutput the sum of the heights of all ordered rooted trees modulo 109+7. Sample
NotesThere are exactly two ordered rooted trees of size 3: 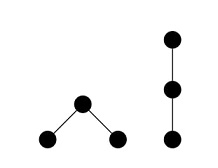 Problem Author: Vadim Barinov Problem Source: Ural Regional Contest Qualifier 2024 Tags: graph theory |
