Граница Лилипутии представляет собой выпуклый многоугольник с ненулевой площадью. В вершинах этого многоугольника расположены сторожевые башни. Эта граница слишком длинная, и она дорого обходится Лилипутии, поэтому правительство страны решило пересмотреть ее и сделать короче. Стоит отметить, что они хотят не строить новые сторожевые башни, а использовать существующие как часть новой границы.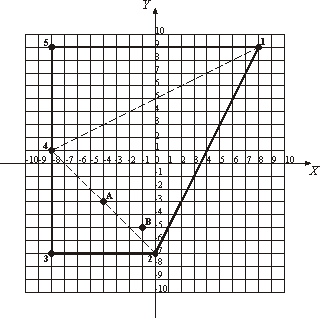

Каждый день пограничники осматривают границу. Они переходят с одной сторожевой башни на другую, преодолевая границу по часовой стрелке. Сторожевые башни пронумерованы от 1 до N в соответствии с порядком этого обхода. После пересмотра границы порядок обхода по часовой стрелке должен сохраниться, а площадь Лилипутии должна оставаться ненулевой.

Например, граница, показанная на рисунке (оси указаны в километровом масштабе), обходится по маршруту 1 - 2 - 3 - 4 - 5 - 1, длина которого составляет 57.89 километра. Чтобы сделать границу как можно короче, Лилипутия должна пересмотреть ее таким образом, чтобы она обходилась по маршруту 2 - 3 - 4 - 2, тем самым сократив ее длину до 27.31 километра.

Однако в Лилипутии есть ряд исторических памятников, которые являются ее главной гордостью. Во чтобы то ни стало исторические памятники должны остаться в Лилипутии, и они не должны находиться на ее границе. Итак, задача состоит в том, чтобы спроектировать кратчайшую границу, которая сохранит все исторические памятники строго внутри Лилипутии.

На рисунке показаны два исторических памятника, отмеченные буквами «А» и «В». Сохраняя их внутри Лилипутии, можно выбрать кратчайшую границу с траекторией 1 - 2 - 3 - 4 - 1 и длиной 51.78 километра.

Первая строка содержит целые числа N и M – количество сторожевых башен на границе Лилипутии и количество исторических памятников, расположенных на территории Лилипутии (3 ≤ N ≤ 50; 0 ≤ M ≤ 1000).

Следующие N строк содержат координаты сторожевых башен в порядке по часовой стрелке, за ними следуют M строк, которые содержат координаты исторических памятников. Координаты – пары целых чисел X и Y. Координаты задаются в километровом масштабе, и каждая координата не превышает 10000 по модулю. Все сторожевые башни расположены в разных точках.

Выведите минимально возможную длину новой границы Лилипутии (в километрах) с точностью не менее двух цифр после десятичной точки.