| ENG RUS | Timus Online Judge |
1772. Лыжни для роботовОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Очередной этап кубка мира по лыжным гонкам среди роботов было решено
провести на лыжной базе «Уктус» в Екатеринбурге.
Лаборатория профессора Попова выставила на гонку новейшего робота NS6,
нейронные сети которого были хорошо обучены классическому
лыжному ходу. С жеребьёвкой ему не повезло: на старт он вышел одним из
последних, когда вся трасса уже была завалена не доехавшими до финиша
участниками. Это оказалось серьёзной проблемой: чтобы объехать
неожиданные препятствия, роботу придётся переходить со своей лыжни на
одну из свободных. Для этого он будет останавливаться и идти боком, теряя
драгоценное время. Чтобы перейти со своей лыжни на соседнюю, роботу придётся потратить
целую секунду. Зная, в каких местах лежат упавшие роботы, определите, как следует их
объехать, чтобы потратить на это минимальное время. 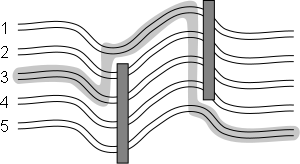 Исходные данныеВ первой строке через пробел записаны целые числа n, s и k
(2 ≤ n ≤ 105; 1 ≤ s ≤ n;
0 ≤ k ≤ 105). Трасса состоит из n лыжней, проложенных параллельно
и идущих от старта до финиша. Лыжни занумерованы числами от 1 до n по порядку.
Робот NS6 стартует с лыжни под номером s. Число k задаёт количество упавших на трассу роботов. В следующих k строках описаны упавшие роботы в порядке от старта к
финишу. В каждой строке через пробел записаны целые числа l и r, означающие,
что очередной робот перегородил все лыжни с номерами от l до r
включительно (1 ≤ l ≤ r ≤ n).
Можно считать, что все упавшие роботы расположены на трассе достаточно
далеко друг от друга (а также от старта) и не помешают роботу NS6
совершать манёвры. Если какой-то робот перегородил крайнюю лыжню, то
объехать его можно только с одной стороны. Никакой робот не перегораживает
все лыжни одновременно. РезультатВыведите минимальное количество секунд, которое робот NS6 должен будет
потратить на переходы с лыжни на лыжню, чтобы объехать всех упавших соперников.
Пример
Автор задачи: Алексей Самсонов Источник задачи: XIV чемпионат Урала по спортивному программированию, 10 апреля 2010 г. Метки: структуры данных |
