| ENG RUS | Timus Online Judge |
2053. БиологияОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Андроид Вася делает курсовую работу по биологии.
В рамках этой работы он изучает пауков, а точнее паутину, которую плетут разные их виды. Вася уже разобрался, как устроена паутина.
Она представляет собой набор точек — узлов паутины, соединенных нитями.
Узлы паутины можно представить как точки, расположенные в одной плоскости.
Нити паутины являются отрезками, которые соединяют узлы.
Важной особенностью этих отрезков является то, что они пересекаются только в узлах паутины. 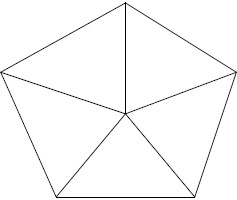 Вася хочет определить, какой вид пауков плетет самую качественную паутину.
Для этого он ввел понятие липкости паутины, определяемое как количество различных ловушек паутины.
Ловушка — это многоугольник без самопересечений и самокасаний, вершинами которого являются узлы паутины, а ребрами — нити. Вася проанализировал несколько паутин, содержащих 16 узлов.
Оказалось, что липкости этих паутин колеблются в промежутке от 5 000 до 300 000.
И сейчас ему интересно, как может выглядеть паутина из 16 узлов с липкостью более 300 000. Исходные данныеВ этой задаче нет входных данных. РезультатВ первых 16 строках выведите координаты узлов паутины в виде пар целых чисел xi, yi (−1000 ≤ xi, yi ≤ 1000).
В следующих 16 строках выведите матрицу смежности паутины — таблицу размера 16 × 16, состоящую из символов «0» и «1».
Матрица должна быть симметрична, ее главная диагональ должна быть заполнена нулями. Любые два узла паутины должны находиться в различных точках.
Узел не может находиться на внутренней точке нити.
Любые две нити паутины могут пересекаться только в их общем узле. Паутина должна иметь липкость строго больше 300 000. Гарантируется, что
такие паутины существуют. Пример
ЗамечанияОтвет в примере приведен лишь для иллюстрации формата (обратите внимание,
что вы должны вывести паутину из шестнадцати, а не из шести узлов).
Паутина из примера соответствует рисунку.
Липкость паутины в примере равняется 21. Автор задачи: Александр Ипатов Источник задачи: XIX Открытый чемпионат Урала по спортивному программированию (апрель, 2015) Метки: необычная задача |
