| ENG RUS | Timus Online Judge |
2191. Кусочно-линейные функцииОграничение времени: 3.0 секунды Ограничение памяти: 256 МБ Вадим — большой фанат кусочно-линейных функций. Они имеют свои ограничения, и не любую функцию можно представить как кусочно-линейную. Вадим вам с радостью расскажет, что это такое. Функция называется кусочно-линейной, если её график можно представить ломаной из N вершин. А именно, она задаётся n парами чисел (x1, y1), (x2, y2), …, (xN, yN), которые являются координатами вершин ломаной. Обязательно должно выполняться условие
Этот набор точек задаёт функцию от одного аргумента, значение которой в xi равно yi, а на промежутках между этими точками она линейная. Область определения такой функции — это отрезок [x1, xN]. Валя придумал свой класс функций с одной переменной, которые он назвал модульными. Модульная функция состоит из N слагаемых, каждое из которых имеет один из двух видов: |ai · x + bi| или −|ai · x + bi|. Здесь x — переменная, а ai и bi — параметры функции, а | … | обозначает взятие по модулю. Таким образом, модульная функция с N слагаемыми имеет вид
Вадим захотел проверить, не хуже ли модульные функции его любимых кусочно-линейных. Он принёс кусочно-линейную функцию с N вершинами. Постарайтесь теперь найти модульную функцию с ровно N слагаемыми, которая будет тождественно равна данной кусочно-линейной на отрезке [x1, xN]. Исходные данныеВ первой строке дано целое число N — количество вершин ломаной (2 ≤ N ≤ 105). Далее идёт n строк, в каждой из которых через пробел даны два целых числа xi, yi — координаты очередной вершины (−105 ≤ xi, yi ≤ 105). Гарантируется, что координаты xi идут строго по возрастанию, то есть
РезультатВыведите в единственной строке модульную функцию из ровно N слагаемых, тождественно равную данной кусочно-линейной функции на отрезке [x1, xN]. Придерживайтесь формата, показанного в примерах. Функция должна состоять из N слагаемых |ai x + bi|, разделённых знаками + и - (коды 43 и 45). Разрешается перед первым слагаемым поставить ведущий минус. Каждое слагаемое должно быть взято по модулю двумя символами | (код 124). Внутри слагаемого должен быть знак + (или -, если bi отрицательно). Левый операнд состоит из вещественного числа ai и переменной x (код 120); знак умножения между ними не нужно писать, он подразумевается. Опускать ai или bi нельзя, даже если ai = 1 или bi = 0; нельзя также опускать левый операнд, если ai = 0.Таких слагаемых должно быть ровно N. Разрешено использовать слагаемые, тождественно равные нулю. Они могут быть записаны как |0x+0|.Размер выходного файла должен быть не больше 8 МБ. Ответ считается правильным, если в любой точке отрезка [x1, xN] значение вашей модульной функции отличается от значения данной кусочно-линейной не более, чем на 0.01. Примеры
ЗамечанияИллюстрация к третьему примеру: 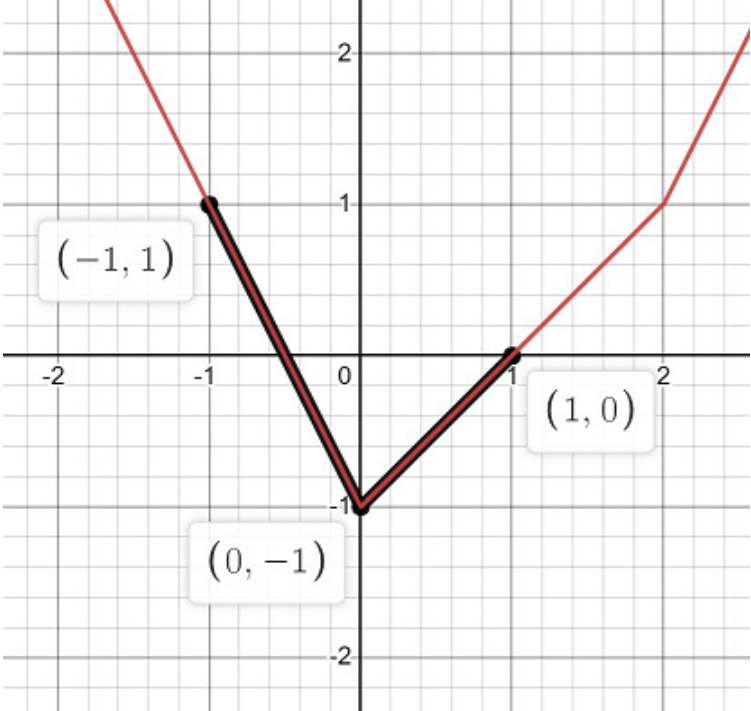 Автор задачи: Валентин Зуев, Вадим Баринов Источник задачи: Квалификационный тур Уральского регионального чемпионата ICPC 2022 Метки: математика |
