| ENG RUS | Timus Online Judge |
2198. Глубокое пониманиеОграничение времени: 1.0 секунды Ограничение памяти: 256 МБ Уже много лет назад Вадим услышал термин «упорядоченное корневое дерево». Он понял, что это такое, но этого недостаточно для «глубокого понимания». Вадим иногда называет высоту корневого дерева «глубиной», и совсем недавно он решил исследовать всевозможные упорядоченные корневые деревья размера N. Нарисовав их все на одном листе бумаги, он подписал «глубину» каждого дерева рядом с соответствующим рисунком. И, наконец, Вадим достиг «глубокого понимания», сложив все написанные числа. Это значение он назвал «величиной глубокого понимания». Ваша цель состоит в том, чтобы найти эту величину по модулю 109+7. Дерево — это связный граф без циклов. Корневое дерево — это дерево с отмеченной вершиной (корнем), его обычно рисуют сверху графа. Высота корневого дерева — наибольшее количество рёбер, по которым можно последовательно пройти из корня, не проходя по одному ребру дважды. Упорядоченное корневое дерево — это корневое дерево, у которого рёбра, выходящие из каждой вершины, упорядочены. Например, следующие два дерева высотой 2 считаются различными: 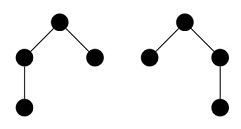 Исходные данныеДано единственное целое число N — размер рассматриваемых деревьев, то есть количество вершин в них (1 ≤ N ≤ 400). РезультатВыведите сумму высот всех упорядоченных корневых деревьев по модулю 109+7. Пример
ЗамечанияВсего есть два упорядоченных корневых дерева размера 3: 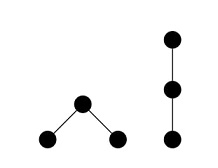 Автор задачи: Вадим Баринов Источник задачи: Квалификационный тур Уральского регионального чемпионата ICPC 2024 Метки: графы |
