Многие программисты СКБ Контур любят добираться до работы на метро — благо, головной офис расположен совсем недалеко от станции Уралмаш. Ну а поскольку сидячий образ жизни требует активных физических нагрузок в свободное от работы время, многие сотрудники — в том числе и Никифор — ходят от дома до метро пешком.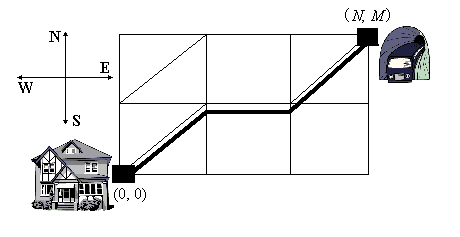

Никифор живёт в таком районе нашего города, где улицы образуют правильную сетку кварталов; все кварталы являются квадратами с длиной стороны, равной 100 метрам. Вход на станцию метро расположен на одном из перекрёстков; Никифор начинает свой путь с другого перекрёстка, который расположен южнее и западнее входа в метро. Естественно, что выйдя из дома, Никифор всегда идет по улицам, ведущим либо на север, либо на восток. Некоторые кварталы, которые встречаются ему на пути, он может также пересечь по диагонали, ведущей из юго-западного угла квартала в северо-восточный. Таким образом, некоторые из маршрутов (ведущих всегда на север, восток или северо-восток), оказываются короче других. Никифора интересует, сколько времени понадобится ему на преодоление кратчайшего маршрута; для этого ему нужно знать его длину.

Вы должны написать программу, которая по имеющейся информации о виде сетки кварталов рассчитывает длину кратчайшего маршрута из юго-западного угла в северо-восточный.

В первой строке находятся два целых числа N и M (0 < N, M ≤ 1000) — размер сетки кварталов с запада на восток и с юга на север соответственно. Никифор начинает путь с перекрёстка, который находится к юго-западу от квартала с координатами (1, 1); станция метро находится к северо-востоку от квартала с координатами (N, M). Во второй строке находится целое число K (0 ≤ K ≤ 100) — количество кварталов, через которые можно пройти наискось. Далее следуют K строк с парами целых положительных чисел, разделённых пробелами — координатами таких кварталов.

Требуется вывести длину кратчайшего пути от дома Никифора до станции метро в метрах, округлённую до целых метров.