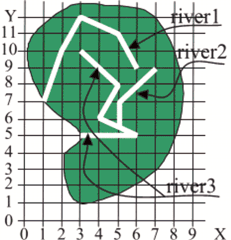You are given a map of rivers of some continent. Every river is shown as a broken line, which begins with a river head and ends either at the point where the river flows into another one, or on the river mouth. The vertexes of the broken line are the turning points of the river-bed, or the points of tributary flow.

We will consider the river basin as a convex polygon of minimum area that contains the river and all its tributaries.

Remark. According to the definition of river basin the same territory may belong to the basins of different rivers.

Sample. A continent with three rivers is shown. The coordinates of the rivers and areas of the basins are given in the table.

Your task is to calculate the maximum among all river basin areas.

The first line contains the number of the rivers N. The rest of the input contains N blocks describing the rivers.

Each block i consists of:

• One line which contains ki – the number of the points in river description;
• ki lines containing pairs of real numbers xj and yj (1 <= j <= ki), separated by space characters – the coordinates of the points that describe the river-bed.

Limitations.
0 < N <= 10, ∑ki <= 1000, -1000 <= xj, yj <= 1000.

Clarifications.

• A river basin includes the river with its tributaries, the tributaries of its tributaries, and so on.
• A river can turn or flow straight at any vertex of the broken line, regardless whether this is a point of tributary flow or not.
• No two rivers intersect or touch, except when a tributary flows into a river.
• No two rivers share the same mouth.
• No two tributaries flow into a river at the same point.
• Tributaries cannot flow into the river's head or mouth.
• The points are given with at most 2 digits after the decimal point.

contains one number – the area of the largest basin calculated with two digit precision.