| ENG RUS | Timus Online Judge |
2020. Traffic Jam in Flower TownTime limit: 1.0 second Memory limit: 64 MB Having returned from Sun City, Dunno told all his friends
that every shorty may have a personal automobile.
Immediately after that so many citizens took a fancy of becoming
road-users, that Bendum and Twistum had to make a mass production
of cars on soda water with syrup. Now traffic jams from several cars
occasionally appear on the crossing of Bell-flower Street and Daisy Street. Bell-flower Street goes from the South to the North and has two driving paths.
It has the right driving, i. e. automobiles move from the South to the North
on the Eastern path and from the North to the South on the Western path.
Daisy Street is single-pathed, and it is perpendicular to Bell-flower Street.
There is one-way movement on it, but its driving direction
is organized in such a way that automobiles drive away from the crossroad
in two opposite directions (see the picture). 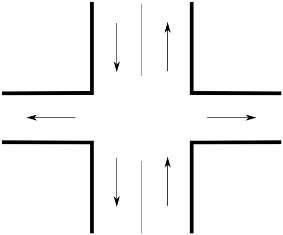 Yesterday on his way home Dunno saw cars standing in a traffic jam
on Bell-flower Street from different sides of the crossing with Daisy Street.
Some of the drivers wanted to go forward, some wanted to turn right or left.
An automobile can pass the crossing in one second,
but if the driver is turning left, he first have to let pass
all oncoming vehicles, going forward and to the right.
How many seconds did it take all the cars to pass the crossing,
providing that no other cars drove up to the crossing? InputThe first line contains the sequence of symbols “F”, “L” and “R”,
describing directions in which drivers who arrived to the crossing
from the South wanted to go. “F” stands for those drivers who were
going forward, “L” is for those who were turning left,
and “R” is for those who were turning right. Automobiles are listed
in the order from the closest to the crossing to the farthest one.
The second line contains the description of the cars, arrived
to the crossing from the North, in the same form.
Both sequences have length from 1 to 1 000. OutputOutput time in seconds, which took all the cars to pass the crossing. Samples
NotesIn the first example we number the cars from 1 to 5 in the order described
in the input data. Then in the first second the crossing was passed
by the first and the fourth cars because they didn’t cause an obstruction to each other.
Then the second car was turning left and had to let the fifth car pass.
As a result, at each of the following three seconds only one car passed the crossing,
and their order was as follows: the fifth one, the second one and the third one. In the second example the cars didn’t cause any obstruction to each other and turned simultaneously. Problem Author: Denis Dublennykh (prepared by Nick Burlakov) Problem Source: NEERC 2014, Eastern subregional contest Tags: none |
