| ENG RUS | Timus Online Judge |
2186. Hands Up!Time limit: 2.0 second Memory limit: 256 MB  Captain Smollett is in a fort located at coordinates (0, 0).
From the fort protrude n guns, represented by vectors (xi, yi).
Nearby, at point (a, b), is John Silver, who is represented as a circle with radius r. Captain Smollett will rotate the fort by some angle alpha (0 ≤ alpha < 360) counterclockwise, and all the guns will rotate with the fort.
Then he will shoot k times from a randomly chosen gun.
During each shot, the gun is chosen independently of all previous shots, and guns may be repeated. John Silver will be hit if at least one shot hits him.
Hits on the boundary of the circle also count. Captain Smollett has q questions.
Question number i is as follows: what is the smallest angle alphai to rotate the fort in order to hit John Silver with a probability of at least pi? Find the answers to all of the captain’s questions. InputThe first line contains three integers n, k, q — the number of guns, the number of shots, and the number of questions (1 ≤ n ≤ 105, 1 ≤ k ≤ 10, 1 ≤ q ≤ 105). The next n lines contain two integers xi, yi — the coordinates of the vector representing the i-th gun (−109 ≤ xi, yi ≤ 109, xi2 + yi2 > 0).
It is guaranteed that no two guns point in the same direction. The following line contains integers a, b, r — the coordinates of John Silver and his radius (−109 ≤ a, b ≤ 109, 1 ≤ r ≤ 109).
It is guaranteed that John Silver does not intersect with any gun. The next q lines contain real numbers pi — the desired probabilities from the queries (0 ≤ pi ≤ 1, the number pi has at most 5 decimal places). OutputIn q lines, output one real number alphai — the answer to the i-th question (0 ≤ alphai < 360).
If it is impossible to hit John Silver with the required probability, output −1. Your answer will be considered correct if its absolute or relative error does not exceed 10−3.
Formally, let your answer be a, and the jury’s answer be b. Your answer will be accepted if and only if |a−b|/max(1, |b|) ≤ 10−3. Sample
NotesBelow is an illustration for the first example.
Note that after rotating the fort, the guns may pass through John Silver, and shots from them will still be considered hits. 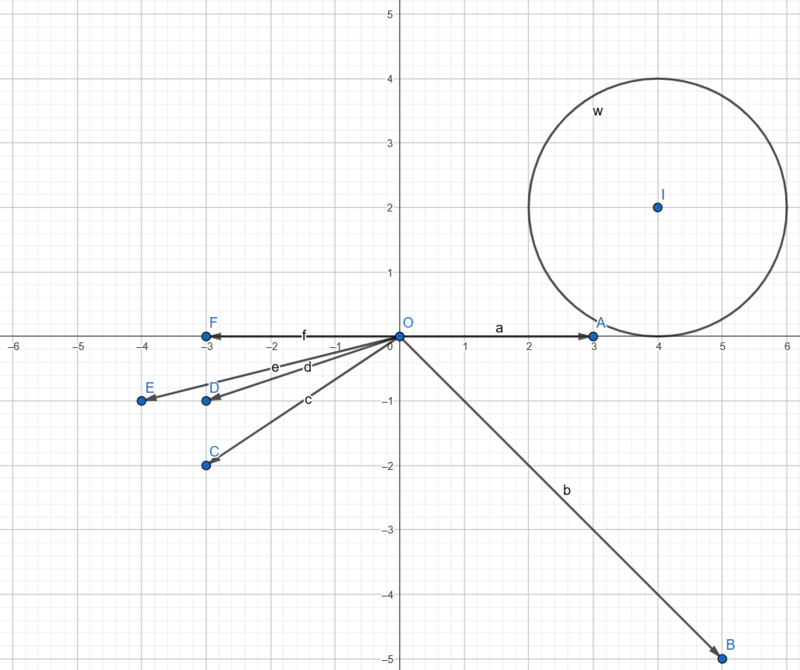 Problem Author: Artyom Kutuzov Problem Source: Ural School Programming Contest 2024 Tags: geometry |
