| ENG RUS | Timus Online Judge |
1024. PermutationsTime limit: 2.0 second Memory limit: 64 MB BackgroundWe remind that the permutation of some final set is a one-to-one mapping of the set onto itself. Less formally, that is a way to reorder elements of the set. For example, one can define a permutation of the set {1,2,3,4,5} as follows: 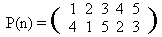 This record defines a permutation P as follows: P(1) = 4, P(2) = 1, P(3) = 5, etc. What is the value of the expression P(P(1))? It’s clear, that P(P(1)) = P(4) = 2. And P(P(3)) = P(5) = 3. One can easily see that if P(n) is a permutation then P(P(n)) is a permutation as well. In our example (check it by yourself) 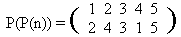 It is natural to denote this permutation by P2(n) = P(P(n)). In a general form the definition is as follows: P(n) = P1(n), Pk(n) = P(Pk-1(n)). Among the permutations there is a very important one — that moves nothing: 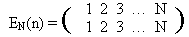 It is clear that for every k the following relation is satisfied: (EN)k = EN. The following less trivial statement is correct (we won’t prove it here, you may prove it yourself incidentally): Let P(n) be some permutation of an N elements set. Then there exists a positive integer k, that Pk = EN. The least positive integer k such that Pk = EN is called an order of the permutation P. ProblemThe problem that your program should solve is formulated now in a very simple manner: “Given a permutation find its order.” InputThe first line contains the only integer N (1 ≤ N ≤ 1000), that is a number of elements in the set that is rearranged by this permutation. In the second line there are N integers of the range from 1 up to N, separated by a space, that define a permutation — the numbers P(1), P(2),…, P(N). OutputYou should write the order of the permutation. You may consider that an answer shouldn’t exceed 109. Sample
Problem Author: Nikita Shamgunov Problem Source: Ural State University Internal Contest October'2000 Junior Session Tags: mathematics |
