| ENG RUS | Timus Online Judge |
1031. Railway TicketsTime limit: 1.0 second Memory limit: 64 MB The railway line “Yekaterinburg-Sverdlovsk” with several stations has been built. This railway line can be represented as a line segment, railway stations being points on it. The railway line starts at the station “Yekaterinburg” and finishes at the station “Sverdlovsk”, so stations are numbered starting from “Yekaterinburg” (it has number 1) and “Sverdlovsk” is the last station. 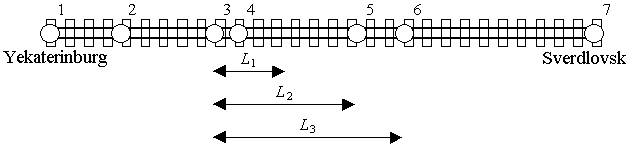 Cost of the ticket between any two stations depends only on a distance between them. The prices for the tickets are specified in the following table.
Direct tickets from one station to another can be booked if and only if the distance between these station does not exceed L3. So sometimes it is necessary to book several tickets for the parts of the whole way between two required stations.
For example, on the railway line shown at the figure above there are seven stations. The direct ticket from the second station to the sixth one can not be booked. There are several ways to pay for the travel between these stations. One of them is to book two tickets: one ticket at price C2 to travel between the second and the third stations, and other at price C3 to travel between the third and the sixth stations. Note, that though the distance between the second and the sixth stations is equal to 2L2, the whole travel can not be paid by booking two tickets at price C2, because each ticket is valid for only one travel and each travel should start and end only at stations.
Your task is to write a program, that will find the minimal cost of the travel between two given stations. InputThe first line contains integers L1, L2, L3, C1, C2 and C3 OutputOutput the minimal travel cost between two given stations. Sample
Problem Author: Pavel Zaletsky Problem Source: Ural Collegiate Programming Contest '99 Tags: dynamic programming |
