| ENG RUS | Timus Online Judge |
1065. FrontierTime limit: 2.0 second Memory limit: 64 MB Lilliputian frontier is a convex polygon with non-zero area.
The vertices of this polygon are guard towers, which are
connected by straight lines.
This frontier is too long and expensive for Lilliputia to maintain;
therefore the Lilliputian government has decided to revise it to make it shorter.
However, they don't want to build new guard towers, but to use existing
ones as a part of a new frontier. 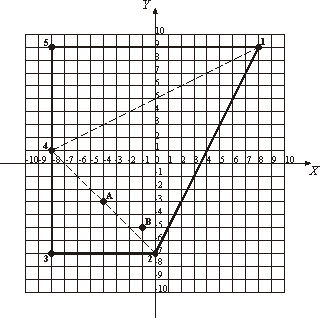 Each day frontier guards inspect the frontier. They go from one guard tower to the next one, traversing the frontier clockwise. Guard towers are numbered from 1 to N according
to this inspection order. Frontier revision should not change this way of inspection and the area of Lilliputia shall remain non-zero.
For example, the frontier that is shown on the picture (axes are in kilometer scale) is traversed by 1 - 2 - 3 - 4 - 5 - 1
route, which is 57.89 kilometers long. To make the frontier as short as possible Lilliputia should revise it so that the frontier is traversed by
2 - 3 - 4 - 2 route, thus reducing its length to 27.31 kilometers. However, Lilliputia has a number of historical monuments which are its major pride. The historical monuments shall be kept inside Lilliputia at any cost and they should not end up on the frontier. So, the task is to design the shortest frontier that will preserve all historical monuments inside Lilliputia. On the sample picture two historical monuments marked “A” and “B” are shown. The desire to keep them inside Lilliputia will lead to the shortest frontier with a traverse path
1 - 2 - 3 - 4 - 1 having 51.78 kilometers in length. InputThe first line contains integers N and M that are a total number
of guard towers on the Lilliputian frontier and a total number
of historical monuments that are situated inside Lilliputia (3 ≤ N ≤ 50; 0 ≤ M ≤ 1000). Next N lines contain guard towers' coordinates in a clockwise order followed by M lines that contain historical monuments' coordinates. All coordinates
are represented as two integers (for X and Y correspondingly) separated by a space. Coordinates are given in a kilometer scale and each coordinate
does not exceed 10000 by an absolute value. All guard towers are located at distinct points. OutputOutput the minimal possible length of the Lilliputian frontier (in kilometers) accurate to two digits to the right of the decimal point. Samples
Problem Source: 2000-2001 ACM Northeastern European Regional Programming Contest Tags: geometry graph theory |
