| ENG RUS | Timus Online Judge |
1066. ГирляндаОграничение времени: 2.0 секунды Ограничение памяти: 64 МБ 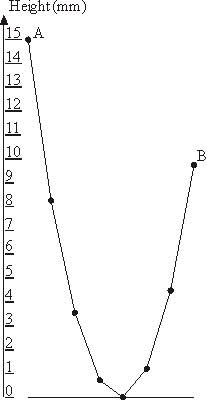 Новогодняя гирлянда, подвешенная за концы, состоит из нескольких ламп, прикрепленных к общему проводу. На концах гирлянды также есть лампы. Провод провисает под весом ламп определенным образом: каждая лампа висит на высоте, которая на 1 миллиметр ниже средней высоты двух соседних ламп. Самая левая лампа висит на высоте A миллиметров над землей. Определите наименьшую возможную высоту B самой правой лампы, чтобы ни одна лампа в гирлянде не лежала на земле, хотя некоторые из ламп могут касаться земли. В этой задаче не нужно учитывать размер ламп. Пронумеровав лампы целыми числами от 1 до N и обозначив высоту i-й лампы в миллиметрах как Hi, получим следующие уравнения:
На рисунке показан пример гирлянды с 8 лампами, где A = 15 и B = 9.75. Исходные данныеЕдинственная строка содержит числа N и A. N – целое число, представляющее количество ламп в гирлянде (3 ≤ N ≤ 1000), A – вещественное число, представляющее высоту самой левой лампы над землей в миллиметрах (10 ≤ A ≤ 1000). РезультатВыведите вещественное число B с точностью не менее двух знаков после десятичной точки – наименьшую возможную высоту самой правой лампы. Примеры
Источник задачи: 2000-2001 ACM Northeastern European Regional Programming Contest Метки: математика |
