| ENG RUS | Timus Online Judge |
1121. BranchesTime limit: 1.0 second Memory limit: 64 MB SKB Kontur has a lot of branches scattered all over the city. The company management decided to create a guide that will help clients to choose which of the branches they need. You are asked for help in this work. The city is represented in the form of a grid of blocks. Each block is a square whose sides are streets and whose corners are cross-roads. We suppose that all branches are located exactly at cross-roads. The branches of SKB Kontur are of different types: service centers, warehouses, shops, training centers and so on. Let's mark service centers with number 1, warehouses with number 2, shops with number 4, training centers with number 8 and so on. There are not more than 11 types of branches, and two branches of the same type cannot be located at the same cross-road. Each cross-road is assigned a number equal to the sum of numbers with which the branches located at this cross-road are marked. Crossroads at which there are no branches of SKB Kontur are assigned 0. 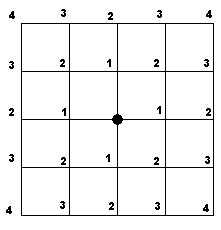 Let the distance between two cross-roads be equal to the number of street segments
which one has to go from the first cross-road to the second (see picture).
For example, the distance from a corner of a block to the opposite corner
of this block is 2.
For each cross-road at which there are no branches of SKB Kontur
you have to find the sum of the numbers corresponding to the types of
the branches nearest to this cross-road.
For example, suppose that there are no branches at a given cross-road and at
distance 1 from it, there is a branch of type 16 at distance 2,
there are also two branches of type 8 and one of type 4 at distance 2
in other directions and there are no more branches at distance 2 from
this cross-road.
Then we should output number 28=16+8+4 for this cross-road.
We do not take into consideration branches that are at distances greater
than 5 from a given cross-road.
Thus, if a cross-road does not have branches of SKB Kontur that
are located at distances less than 6 from it then we should output
0 for this cross-road. InputThe first line contains positive integers H and W not exceeding 150.
They are numbers of "vertical" and "horizontal" streets, correspondingly.
The next H lines contain W numbers each, the i-th number in the j-th line
describing types of the branches located at the cross-road of the
i-th "vertical" and the j-th "horizontal" street. OutputYou should output H lines containing W numbers each,
the i-th number in the j-th line being equal to
the sum of the numbers corresponding to the types of
the branches nearest to the corresponding cross-road
if there are no branches at this cross-road and −1 otherwise. Sample
Problem Author: Leonid Volkov, Alexander Somov Problem Source: USU Open Collegiate Programming Contest October'2001 Junior Session Tags: none |
