| ENG RUS | Timus Online Judge |
1133. Fibonacci SequenceTime limit: 1.0 second Memory limit: 64 MB 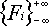 is an infinite sequence of integers that satisfies to Fibonacci condition Fi + 2 = Fi + 1 + Fi for any integer i.
Write a program, which calculates the value of Fn for the given values of Fi and Fj. InputThe input contains five integers in the following order: i, Fi, j, Fj, n. −1000 ≤ i, j, n ≤ 1000, i ≠ j, −2·109 ≤ Fk ≤ 2·109 (k = min(i, j, n), …, max(i, j, n)). OutputThe output consists of a single integer, which is the value of Fn. Sample
NotesIn the example you are given: F3 = 5, F−1 = 4; you asked to find the value of F5. The following Fibonacci sequence can be reconstructed using known values: …, F−1 = 4, F0 = −1, F1 = 3, F2 = 2, F3 = 5, F4 = 7, F5 = 12, … Thus, the answer is: F5 = 12. Problem Source: Quarterfinal, Central region of Russia, Rybinsk, October 17-18 2001 Tags: number theory |
