| ENG RUS | Timus Online Judge |
1377. Lara CroftTime limit: 1.0 second Memory limit: 64 MB A cemetery has a form of rectangle. There are N rows of graves, M ones in each row. The cemetery is enclosed with a high fence. Lara Croft has penetrated into the cemetery through the sap at the Northwestern corner. It takes one night for Lara to dig a subway under one of the graves. If there is an intact grave straight ahead then Lara will lengthen the passage during the next night and will ravage the grave. If there is a cemetery fence or a ravaged grave on the way, then Lara will turn 90 degrees clockwise and will continue with her questionable affairs. Treasures are located in two graves only. And we exactly know in which ones. But Lara doesn't. Lara has bought a package of champagne today. It means, that today she has found one of those graves. We wonder how long will it take her to find the other one?
InputThe first line contains integers N and M that are the sizes of the cemetery (2 ≤ N, M ≤ 100).
The North-Western grave has coordinates (1, 1) and the South-Eastern one — (N, M). Lara starts with the grave (1, 1) moving to the East, i.e. towards the grave (1, 2). The second and the third lines contain integers (r1, c1) and (r2, c2) that are the treasure graves coordinates ( OutputOutput an amount of days that Lara will spend reaching for another grave with treasures.
Sample
NotesIn the example Lara will find the treasures on the 9'th and the 15'th days. 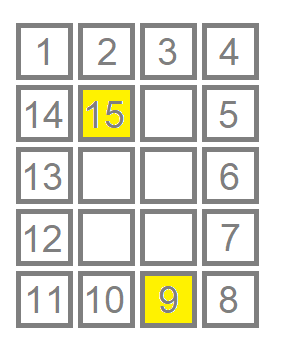 Problem Author: Stanislav Vasilyev Problem Source: IX Urals Programming Contest. Yekaterinburg, April 19-24, 2005 Tags: none |
