| ENG RUS | Timus Online Judge |
1529. Game of SquaresTime limit: 5.0 second Memory limit: 64 MB Alice and Bob are playing with k-dimensional rectangular parallelepiped
consisting of n1 × n2 × … × nk unit hypercubes.
They make moves in turn. Alice chooses some unit hypercube, and cuts
the parallelepiped through the center of this hypercube with all possible
planes that are parallel to its sides. All unit hypercubes that were
cut by at least one plane are removed, and what remains is a series of smaller
rectangular parallelepipeds. It is required that at least one of those
small parts has edge lengths that are pairwise relatively prime with
the corresponding edge lengths of the original parallelepiped. It is also allowed
to cut the parallelepiped in such way that no parts remain.
Afterwards, each player chooses any of remaining parallelepipeds, and cuts
it as described above. After a cut every parallelepiped is left,
and making the turn the player can choose any of them.
The player who can't move loses. Assuming
both players play optimally, who will win?
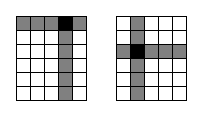 Let's consider an example. Assume that k = 2, and we have a 6 × 5
rectangle. By cutting the hypercube at (1, 4) we get two parts:
5 × 1 and 5 × 3. As the second part's (as well as first part's,
but that's not important) edge lengths are relatively prime with
the edge lengths of the original rectangle (5 is relatively prime with 6 and
3 is relatively prime with 5), this is a possible move. However,
cutting the hypercube at (3, 2) is not a possible move, because each of the remaining
parts (2 × 1, 3 × 1, 2 × 3, 3 × 3) doesn't satisfy
the condition above.
InputThe first line of the input contains an integer k (1 ≤ k ≤ 8),
the second line contains k integers n1, n2, … nk,
1 ≤ (n1+1) × (n2+1) × … × (nk+1) ≤ 10000.
OutputOutput the number of the winning player to the first line of output
(1 for Alice, 2 for Bob). In case Alice wins the game, output the
first move that leads her to the win to the second line of output.
The move is described by k numbers, 1-based coordinates of the
cut hypercube. In case there're several possible moves that lead her
to the win, output the lexicographically smallest one.
Samples
Problem Author: Dmitry Gozman Problem Source: Dmitry Gozman Contest 1, Petrozavodsk training camp, January 2007 Tags: game |
