| ENG RUS | Timus Online Judge |
1554. Multiplicative FunctionsОграничение времени: 2.0 секунды Ограничение памяти: 64 МБ In number theory, a multiplicative function is an arithmetic function F(n)
of the positive integer n with property that F(1) = 1 and whenever a and b
are coprime The function E(n) defined by E(n) = 1 if n = 1 and = 0 if n > 1, is sometimes
called multiplication unit for Dirichlet convolution or simply the unit function.
If F and G are two multiplicative functions, one defines a new multiplicative
function F * G, the Dirichlet convolution of F and G, by
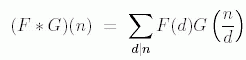 where the sum extends over all positive divisors d of n. With this operation,
the set of all multiplicative functions turns into an abelian group; the identity element is E.
from Wikipedia, the free encyclopedia
In this task you have to find the inverse of a multiplicative function.
To cope with overflow problem, we define arithmetic functions as:
F: N * G = G * F = E.
You are given the first N values of function F, you need to find the first N values of
the inverse function G.
Исходные данныеIn the first line of the input one number N is written (1 ≤ N ≤ 104).
In the second line values F(1), F(2), F(3), …, F(N) are listed. Numbers are
separated by spaces. (Each value is nonnegative and doesn't exceed 2006.)
РезультатIn the first line of the output print first N values of inverse function G,
separated by spaces: G(1), G(2), …, G(N).
Пример
Источник задачи: Novosibirsk SU Contest. Petrozavodsk training camp, September 2007
Метки: теория чисел |
