| ENG RUS | Timus Online Judge |
1674. Drunk KingTime limit: 1.0 second Memory limit: 64 MB Drunk king is a piece which moves as a usual chess king (i. e. to one of eight adjacent cells), but cannot make two consecutive moves in the same direction. Drunk king stands in an upper-left corner of an N × M chessboard and wants to visit each cell exactly once and return to initial position. His path must have no self-intersections. Here are the examples of correct tours: 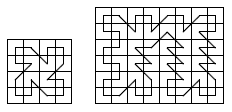 Help the king to find the required tour. InputThe only input line contains 2 integers: N and M
( OutputIn the first line output “Yes” or “No” depending on whether the required tour exists. If the tour exists, output it in the next 2N − 1 lines with symbols “o” (ASCII code 111), “|” (code 124), Samples
Problem Author: Igor Chevdar Problem Source: Ural SU Contest. Petrozavodsk Summer Session, August 2008 Tags: hardest problem |
