| ENG RUS | Timus Online Judge |
1707. Hypnotoad's SecretTime limit: 5.0 second Memory limit: 64 MB  Everybody loves Hypnotoad! Its show is one of the most popular on TV!
It is true that after the show nobody remembers what it was about and even what
they have been doing during all that time. However, this does not prevent
the numerous fans of Hypnotoad from enjoying their favorite show. In order to study the amazing properties of Hypnotoad, Professor Farnsworth
constructed a special device, which trapped and scanned its waves. He found out
that at each time moment Hypnotoad's eyes could be in one of n states.
Professor denoted those states by the numbers 0, 1, …, n−1
for simplicity. The states of the eyes changed according to one of several
linear laws. There were m such laws and each of them could be specified by
five integers:
s0, t0, Δs, Δt, k.
When Hypnotoad “worked” according to such a law, its left eye switched to
the state si and its right eye switched to
the state ti successively
for all integers i from 0 to k−1, where si = (s0 + i Δs) mod n, ti = (t0 + i Δt) mod n. After several weeks of research, Farnsworth understood that Hypnotoad's waves
could be used to learn many secrets of the Universe. For example, Hypnotoad could
see the dark matter and extract information from black holes. In order to see
the same way Hypnotoad saw, Professor constructed another device that emulated
“hypnosight”: each of its four oculars could stay in one of the n
states changing according to linear laws. Farnsworth carried out a series of
experiments and decided to draw a diagram in which he would mark for every possible state
of the device whether Hypnotoad's eyes could be in states similar to the states of
the oculars. Help Professor automate this process.
One experiment is described by nine integers:
a0, b0, c0, d0,
Δa, Δb, Δc, Δd, q.
For all integer values of j from 0 to q−1, the oculars successively switch to
the following states:
aj = (a0 + j Δa) mod n, bj = (b0 + j Δb) mod n, cj = (c0 + j Δc) mod n, dj = (d0 + j Δd) mod n. For every state of the device (aj, bj,
cj, dj), it is required to determine
whether Hypnotoad's eyes can be in a state
(si, ti) such that
min(aj, bj) ≤
si ≤
max(aj, bj), min(cj, dj) ≤ ti ≤ max(cj, dj). InputIn the first line you are given the number n of states of Hypnotoad's eyes
and the number m of laws of their behavior
(1 ≤ n ≤ 5000, 1 ≤ m ≤ 1000).
Each of the following m lines contains the integers
s0, t0, Δs, Δt, k,
which specify the law according to which the states of the eyes are switched
(0 ≤ s0, t0, |Δs|,
|Δt| ≤ n−1; 1 ≤ k ≤ 567).
In the next line you are given the number p of experiments
(1 ≤ p ≤ 345). Each of the following p lines contains the integers
a0, b0, c0, d0,
Δa, Δb, Δc, Δd, q,
which describe the experiment
(0 ≤ a0, b0, c0,
d0, |Δa|, |Δb|, |Δc|,
|Δd| ≤ n−1; 1 ≤ q ≤ 345).
OutputOutput p lines, one line per experiment. For each experiment, determine
its result: the set of numbers xj for j = 0, 1, …, q−1.
In this set, xj = 1 if Hypnotoad's eyes can be in a state complying
with the corresponding state of the device and xj = 0 otherwise.
If q ≤ 20, output all xj in a row without spaces.
If q > 20, output one number equal to
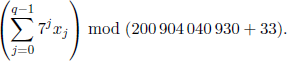 Sample
Problem Author: Dmitry Ivankov Problem Source: The 13th Urals Collegiate Programing Championship, April 04, 2009 Tags: data structures |
