| ENG RUS | Timus Online Judge |
1750. Pakhom and the GullyTime limit: 1.0 second Memory limit: 64 MB Pakhom stands at the point S and wants to reach the point T to buy the land there. But he noticed a gully, which represents a polyline ABC. What is the length of the shortest path Pakhom should walk if he doesn't want to fall into the gully? 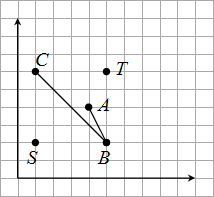 InputThe first line contains the number of testcases n (1 ≤ n ≤ 5000). Each of the next n lines contains one testcase. Each testcase is written as 10 space-separated integers: xS, yS, xT, yT, xA, yA, xB, yB, xC, yC, the coordinates of the points S, T, A, B, and C, respectively. All points within the test case are different. Points S and T don't belong to the polyline ABC. All numbers in test cases don't exceed 10 by absolute value. OutputFor each test case output the answer on a separate line. The answer should be precise up to 10−6. Sample
Problem Author: Petr Lezhankin Problem Source: Ufa SATU Contest. Petrozavodsk Summer Session, August 2009 Tags: geometry |
