| ENG RUS | Timus Online Judge |
1805. Chapaev and a Cipher GrilleTime limit: 0.5 second Memory limit: 64 MB When searching the Whites' deserted headquarters, Petka and Chapaev found
several n × n squares filled with letters. Chapaev supposed that
the Whites were communicating secretly by using a cipher grille and the
squares were ciphered messages.
 A cipher grille is an n × n paper square with windows made by cutting
out n2/4 cells. Putting the grille on a paper sheet of the same size,
the coder writes the first n2/4 symbols of a message in the windows.
After that he turns the grille clockwise by 90 degrees. He writes the next
n2/4 symbols of the message in the windows and turns the grille by 90
degrees again. Then he writes the following n2/4 symbols, turns the
grille one more time, and writes the last n2/4 symbols of the message.
Each turn of the grille covers all the symbols written earlier and opens
empty cells.
Despite searching the headquarters thoroughly, Petka and Chapaev found no
cipher grilles. Evidently, the Whites had destroyed them before leaving
the premises. On the next day Anka noticed that there was an integer k
written on a wall of the headquarters. She informed Chapaev at once,
and he surmised that the Whites had used the kth cipher grille in the
lexicographic order. In order to decipher the messages, they had to
make such a grille.
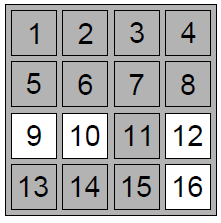
Every n × n cipher grille can be coded as an n × n matrix
consisting of zeros and ones in which ones denote windows and zeros
denote other cells. We say that a matrix a is lexicographically smaller
that a matrix b (both matrices are of the size n × n) if there
exists a number i such that the first i cells of the matrices a
and b coincide, the (i+1)th cell of the matrix a contains zero,
and the (i+1)th cell of the matrix b contains one. The cells
of matrices are numbered as in the picture.
InputThe only line contains the integers n and k (4 ≤ n ≤ 10;
n is even; 1 ≤ k ≤ 1018). It is guaranteed that
k does not exceed the total number of cipher grilles
of size n × n.
OutputOutput the grille Chapaev had to make in order to read the Whites'
messages.
Sample
Problem Author: Alexander Ipatov Problem Source: NEERC 2010, Eastern subregional contest Tags: none |
