| ENG RUS | Timus Online Judge |
1950. Martian FarmlandsTime limit: 1.0 second Memory limit: 64 MB 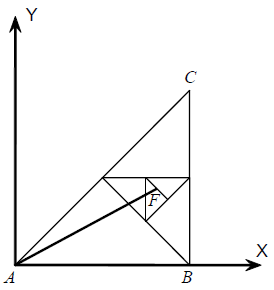 Alexey Ivanovich decided to sell his farmland on Mars and return
to his dear Venus. His farmland has the shape of a flat rectangular
triangle ABC, which contains a narrow straight irrigation channel AF.
Unfortunately, Alexey Ivanovich didn’t manage to find a buyer quickly.
It turned out that cottagers wanted to buy only farmlands with
through irrigation channel, i.e., a channel having exactly two common
points with a border line of a farmland. Alexey Ivanovich realized that he could
divide his farmland into several smaller ones and sell them separately. He
decided to divide the initial farmland into two identical
triangular farmlands of the same shape by drawing an altitude to the
hypotenuse. Then he would consider the half containing F inside and
do the same—draw another altitude to the hypotenuse and consider
the smaller farmland containing point F. The process would go on until point
F is on another altitude, or until the size of the new farmlands is negligibly small. Help Alexey Ivanovich to count the total area of all resulting farmlands which
he will be able to sell. InputLet’s introduce the coordinates in such a way that point A has the coordinates (0, 0),
point B has the coordinates (10, 0) and point C has coordinates (10, 10).
The only line contains real numbers x and y that are coordinates of point F (0 < y < x < 10).
Numbers x and y are specified with at most three digits after decimal point. OutputOutput the total area of the farmlands fit for sale with absolute or relative
error of at most 10−3. Sample
Problem Author: Andrey Demidov Problem Source: Open Ural FU Personal Contest 2012 Tags: none |
