| ENG RUS | Timus Online Judge |
2019. Pair: normal and paranormalTime limit: 1.0 second Memory limit: 64 MB If you find yourself in Nevada at an abandoned nuclear range during Halloween
time, you’ll become a witness of an unusual show. Here Ghostbusters hold
annual tests for new versions of their proton packs.
There are n Ghostbusters and n portable traps with ghosts,
all are located on a semicircle. Each trap contains exactly one ghost.
The ghosts may be of different types,
but each Ghostbuster can neutralize with his weapon only one type
of the evil spirits. On the count of three all ghost traps open at once and all
Ghostbusters start to fire. Of course, each Ghostbuster shoots at the
ghost, which his proton gun is able to neutralize. The most important thing
here is not to cross proton beams of the guns. 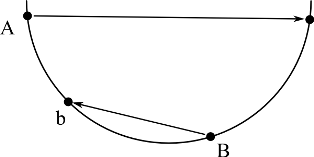 You know positions of all Ghostbusters and all the traps in this year’s tests.
For each Ghostbuster determine which ghost he should shoot at, so that
all the ghosts are neutralized and no two gun beams cross.
You can assume that all proton beams are in the same horizontal plane and
they don’t shoot ghosts through in case of a hit. InputIn the first line there is an integer n that is the number of Ghostbusters
(1 ≤ n ≤ 5 000). In the second line the sequence of 2n Latin letters
is written, describing the allocation of the Ghostbusters and the traps
on the semicircle. Uppercase letters correspond to the Ghostbusters and
lowercase letters correspond to the traps. For example, “a” stands for a trap
with the ghost of type “a”, while “A” stands for the Ghostbuster
with the gun neutralizing ghosts of type “a”.
The sequence has exactly n lowercase letters and exactly
n uppercase letters. OutputIf the problem has a solution, output n space-separated integers
g1, g2, …, gn, where gi is the number of the ghost
i-th Ghostbuster should shoot at. Both Ghostbusters and ghosts are numbered with
integers from 1 to n in the order of their positions along the semicircle.
All gi must be pairwise different. If the problem has several
solutions, output any of them. If the problem has no solution,
output “Impossible”. Samples
Problem Author: Denis Dublennykh (prepared by Oleg Merkurev) Problem Source: NEERC 2014, Eastern subregional contest Tags: none |
