| ENG RUS | Timus Online Judge |
2148. Insane ShotTime limit: 0.5 second Memory limit: 256 MB Sher loves playing a popular browser io-game. Playing it every day, Sher achieved huge results, and now he is a part of the strongest e-sports team. The game is a 2D Battle Royale. The battlefield is a top-down plane with a coordinate system. There are multiple objects such as buildings, rocks, trees, barrels, bushes, bridges, rivers and cylindrical tanks. Being able to aim and shoot sniper rifles over long distances is considered the superior skill in this game. Sher, of course, has mastered it. So he tries to develop a new skill of shooting enemies by ricocheting bullets off of deflecting surfaces. In this game, every metal surface deflects bullets. Performing a ricochet is illustrated in the picture below. At this very moment Sher found himself in a perfect spot for demonstrating his aim: he spotted an enemy and a cylindrical metal tank. Help Sher to shoot the enemy using his new skill. A shot that touches the tank without changing the trajectory of the bullet doesn’t count as skill demonstration. To simplify the problem, let’s presume that there’s nothing on the field except for the tank, which is a circle, and two players, who are at the same distance from the tank; the players are points on the plane. The angle of incidence is equal to the angle of reflection. 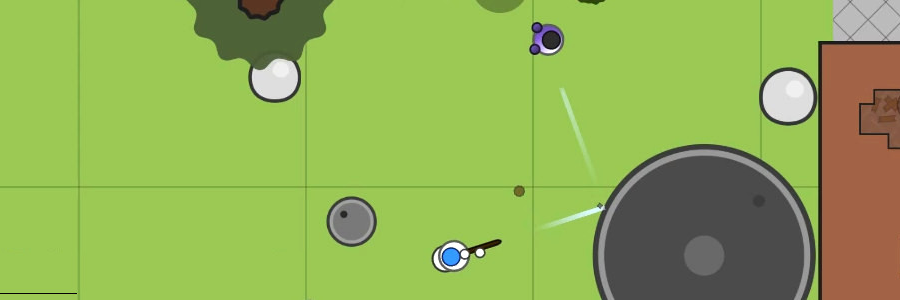 InputThe first line contains three space-separated integers — coordinates of the center of the tank and its radius. The radius is positive. The second line contains two space-separated integers — Sher’s coordinates. The third line contains two space-separated integers — enemy’s coordinates. All integers do not exceed 3000 by absolute value. It is guaranteed that Sher and the enemy are located in different points outside the tank. It is guaranteed that distances from Sher to the tank and from the enemy to the tank are equal. OutputIf the answer doesn’t exists, output one line “ No way” (without quotes). Otherwise, output two space-separated numbers — coordinates of the point. The answer is considered correct if the distance from the point to the center of the tank and its radius differ by at most 10−6, the angle of incidence and the angle of reflection differ by at most 10−6 and the trajectory of the shot doesn’t contain inner points of the tank.Samples
Problem Author: Kirill Meshcheryakov Problem Source: Ural School Programming Contest 2019 Tags: geometry |
