| ENG RUS | Timus Online Judge |
NEERC, Центральный подрегион, Рыбинск, октябрь 2002
Соревнование завершено
I. Посадка на астероидОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ 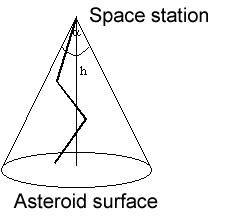 Управляемый зонд запущен с космической станции, находящейся на расстоянии h от поверхности большого астероида. Зонд должен совершить посадку на астероид. Зонд может двигаться строго по прямой на фиксированное расстояние d, после чего он получает новую команду со станции. Команда определяет новое направление движения. Каждое движение зонда должно приближать его к поверхности. Управляющие сигналы станции передаются только внутри конуса, имеющего угол α при вершине. Таким образом, траектория зонда представляет собой ломаную, состоящую из отрезков одинаковой длины, лежащую внутри конуса. Последний отрезок траектории также должен быть длиной d, лежать внутри конуса передачи и заканчиваться на поверхности астероида. Вашей задачей является определить, возможно ли выполнить посадку зонда при выполнении описанных условий. Если посадка возможна, найдите траекторию минимальной длины, включая координаты концов каждого отрезка. Точка посадки также должна быть найдена. Координаты точек декартовы. Оси Ox и Oy лежат на поверхности астероида, ось Oz проходит через космическую станцию. Исходные данныеh (0.5000 ≤ h ≤ 99.9999), d (1.0000 ≤ d ≤ 5.0000), α (угол в радианах, 0.1000 ≤ α ≤ 2.0000). Все числа вещественные и имеют не более 4-х знаков после десятичной точки. Результатn — количество отрезков, составляющих траекторию, или −1, если посадка невозможна x1 y1 z1 x2 y2 z2 … xn yn zn — координаты точек, в которых зонд получает сигналы управления, а также точка посадки. Все координаты должны быть вычислены с точностью 0.0001. Пример
Источник задачи: Четвертьфинальные соревнования ACM ICPC 2002–2003 в центральном регионе России, Рыбинск, октябрь 2002 |
