| ENG RUS | Timus Online Judge |
SPbSU ITMO contest. Petrozavodsk training camp. Winter 2008
Соревнование завершено
D. Definite IntegralОграничение времени: 1.0 секунды Ограничение памяти: 64 МБ Your task is to evaluate the following definite integral:
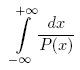 where P(x) = a4 · x4 + a3 · x3 + a2 · x2 + a1 · x + a0. P(x) has no real roots and GCD(P(x), P'(x)) = const. Исходные данныеThe input contains five integers: a0, a1, a2, a3 and a4 separated by whitespace. Each of these numbers does not exceed 106 by absolute value, a4 ≠ 0. РезультатOutput the value of the integral. Assume that the exact value is A and your answer is B. Your answer will be considered correct if and only if at least one of the following statements is true:
Пример
Источник задачи: SPbSU ITMO contest. Petrozavodsk training camp. Winter 2008. |
