| ENG RUS | Timus Online Judge |
NEERC 2008, Eastern subregion quarterfinals
Contest is over
C. Shortest SubchainTime limit: 1.0 second Memory limit: 64 MB 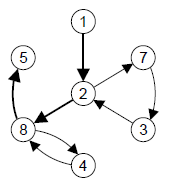 A chain p is given in a directed graph without loops or multiple edges.
It is required to specify its subchain q such that
InputThe chain p is given by the list of its vertices.
The first line contains the number n of vertices in the list, 2 ≤
n ≤ 100000 (thus, the length of the chain is n−1). The
following lines contain n numbers of vertices (they are integers in the
range from 1 to 10000). The numbers are separated by spaces or linebreaks. No
two successive vertices in the list coincide. OutputOutput the vertices of the chain q by giving their numbers separated by a space.
Chain q may consist of single a vertex.
Sample
Problem Author: Vladimir Yakovlev (idea by Magaz Asanov) Problem Source: NEERC 2008, Eastern subregion quarterfinals |
