| ENG RUS | Timus Online Judge |
Ural Championship 2009
Contest is over
C. CrossroadTime limit: 2.0 second Memory limit: 64 MB 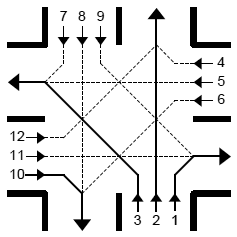 The crossroad of the Lenina Prospect and the 8th of March Street is in the
very center of Yekaterinburg. There is no surprise that traffic jams are quite
common there. In this problem you will help the city to relieve the situation.
The cars approaching the crossroad from one of the four sides divide into
three flows: those turning left, turning right, and going straight. Each of the
12 flows is regulated by a separate traffic light. The traffic lights work in
coordination and can change their states once a minute. Their signals should
not contradict each other. This means that the flows of cars passing the
crossroad according to the traffic light signals should not intersect each
other.
For example, if the straight motion is allowed in the north direction, then the
straight motion from the west side of the crossroad must be forbidden because
it would not be safe. However, the right turn from the west side can be
allowed. Two flows of cars passing the crossroad are considered intersecting
if they have the same final direction or if their trajectories intersect.
In the picture the flows shown by solid lines (numbered 1, 2, 3, and 10)
do not intersect, and each of the remaining flows intersects at least one of
those shown by solid lines.
Assume that 12 integers ni are known that are the
numbers of the cars wishing to pass the crossroad in each of the directions
(which are enumerated from 1 to 12 as shown in the picture). The 12 speeds vi
of passing the crossroad are also known; they are the numbers of cars
that can pass the crossroad in one minute if the passage is allowed. Assume
that new cars don't arrive. Your task is to unload the crossroad in ten
minutes by controlling the traffic lights. The aim is to minimize the maximal
number of cars remaining in one of the 12 flows.
InputThe first line contains 12 integers ni, 0 ≤ ni ≤ 1000.
The second line contains 12 integers vi, 1 ≤ vi ≤ 1000.
OutputOutput the number of cars remaining in the largest flow in ten minutes
if the traffic lights are controlled optimally.
Sample
NotesThe largest number of cars are going from the west to the east
(flow 11), and they should be allowed to move during all 10 minutes. In the
first 4 minutes, the cars arriving from the east can be allowed to move (flows 4 and 5)
because none of them turns the south. In the remaining six minutes, the flow from
the north to the west should be let through (7).
Problem Author: Sergey Pupyrev Problem Source: The 13th Urals Collegiate Programing Championship, April 04, 2009 |
