| ENG RUS | Timus Online Judge |
Ural Regional School Programming Contest 2019
Contest is over
B. Experiment with JuiceTime limit: 4.0 second Memory limit: 256 MB Sasha loves physics. Sasha has no friends. Whether these facts are connected or not, Sasha is very upset about his lack of friends. So he tried to impress Vadim with an experiment. Sasha lives on a plane with a Cartesian coordinate system. He took a convex polygon with n vertices numbered from 1 to n, where the i-th vertex has coordinates (xi, yi), and poured juice inside the polygon, filling it to the brim. Then he brought it to Vadim to demonstrate an experiment. Turns out, Vadim doesn’t like physics and doesn’t care about Sasha’s experiments. So he poked a hole in one of the sides of the polygon (but not in one of its vertices!), the hole is a point with coordinates (x0, y0). All the excess juice poured out of the polygon due to the gravity (gravity is pointed in the direction of decrease of coordinate y). But Vadim wasn’t satisfied yet, so he started rotating the polygon slowly by angles αi around the center of the coordinate system, spilling even more juice. You witnessed it all, but no one could stop Vadim. At least you can reassure Sasha by telling him how much exactly juice remained before and after every rotation. We hope you are a good person, and you’ll succeed at calming Sasha down. InputThe first line contains one integer n — the amount of vertices (3 ≤ n ≤ 105). Next n lines contain two numbers xi, yi each, separated with a space — coordinates of vertices in counter-clockwise order (−105 ≤ xi, yi ≤ 105). Coordinates are given with exactly three digits after the decimal point. The (n+2)-th line contain two numbers x0, y0 each, separated with a space — coordinates of the hole (−105 ≤ x0, y0 ≤ 105). Coordinates are given with exactly three digits after the decimal point. The (n+3)-th line contains an integer q — the amount of rotations (0 ≤ q ≤ 105). The last q lines contain one number αi each — angles of rotations in the order they were performed, counter-clockwise, in degerees (−360 ≤ αi ≤ 360, rotation by −x counter-clockwise is the same as rotation by x clockwise). The angles are given with exactly three digits after the decimal point. It is guaranteed that the polygon is convex, no three vertices lay on the same line, and that the hole is located exactly on the polygon’s side, but not in one of the vertices. OutputOutput q + 1 lines. The first line should contain the area of juice remaining after Vadim poked the hole. Each of next q lines should contain the remaining area of juice after each rotation. The answer is considered correct if absolute or relative error of each number doesn’t exceed 10−4. Sample
NotesIllustration of the example 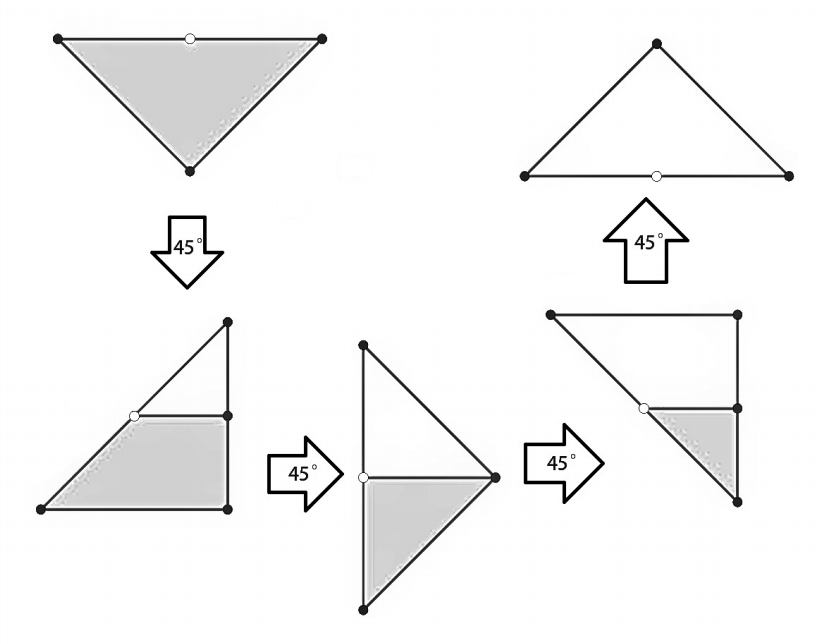 Problem Author: Vadim Barinov Problem Source: Ural School Programming Contest 2019 |
